基于eta/Dynaform发盖外板冲压回弹的数值模拟研究
回弹是影响板料冲压成形质量的一个重要因素,它直接影响着冲压件的尺寸精度以及生产工艺工序。本文以eta/DYNAFORM为实验平台,对发动机罩外板的冲压回弹进行数值模拟,通过对机罩外板拉深成形后的回弹量进行研究,得出机罩外板类零件冲压回弹情况,为研究冲压成形工艺及优化设计方案提供有力手段。
起皱、破裂和回弹是薄板成形中的三种主要质量缺陷,其中回弹是最难控制的,因为回弹的存在会影响冲压件的形状尺寸精度和表面质量。冲压件的最终形状取决于成形后的回弹量,当回弹量超过允许容差后,就成为成形缺陷,进而影响整车装配。国内许多汽车公司正在开展“2mm”工程,即综合装配误差控制在2mm以内;因此,回弹的控制及预测是一个重要的话题。
回弹不仅是工业生产中的一个实际问题,也是长期以来困扰学术界的问题之一。有限元数值模拟技术的引入,为推动回弹问题的解决提供了有利的工具。本文利用有限元技术对我公司某车发动机罩外板(见图1)成形后的回弹变形进行准确预测,研究控制回弹方法以提高成形精度,对于降低发动机罩外板冲压制造成本、保证整车装配质量和缩短新产品开发具有重要的意义。

图1 发动机罩外板实物
有限元法计算回弹的关键技术
回弹是板料成形过程中普遍存在的一种现象,对于诸如覆盖件这类大型高强度薄板零件的冲压成形而言,回弹问题的研究尤为重要。回弹问题在以下两类冲压制件中尤其突出:以弯曲为主要变形方式的类U形弯曲件,如各种梁结构,由于这类冲压件的外形尺寸通常很大,所以又称为大弯曲件;以浅拉深为主要变形方式的小曲率件,如前后门外板、行李箱盖外板和顶盖等,以及与之相应的内覆盖件等。
1.回弹机理
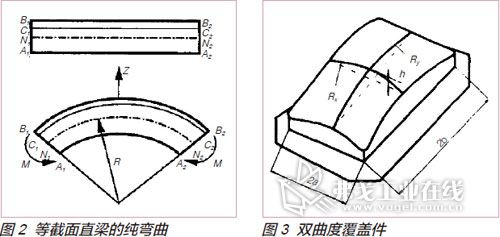
对于弯曲件来说,为说明回弹的形成机理,以等截面梁的纯弯曲为例进行研究。设梁具有一个纵向对称平面,且在这个平面内受到一对弯矩M的作用(见图2)。由于采用平截面假定,两个横截面A1B1和A2B2在弯矩作用下作相对旋转但仍皆垂直于梁的对称平面。于是凸面的纵向纤维受拉伸而凹面B1B2的纵向纤维受压缩。在垂直于对称平面的某一平面N1N2上纤维保持长度不变,称之为中性面,它将梁内受纤维和受压纤维分开。在弯矩M的作用下,材料产生弹塑性变形,卸载后由于弹性变形的恢复,梁的曲率会减少,这种现象就是回弹。
拉深件如图3所示,其中,h为零件中心弧高,Rx、Ry分别为X、Y方向的主曲率半径:Rx=a2/2H,Ry=b2/2H通常来讲,造成成形后的零件发生回弹的主要原因有两个:卸载后,任何弹塑性变形体都伴随有弹性恢复;当板料内外表层纤维进入变形状态时,其芯部仍可能处在弹性状态,造成卸载后的宏观回弹。
2.模型的建立
模型的建立包括冲压成形的力学模型及有限元模型的建立,由于实际的冲压过程非常复杂,因此在仿真时必须予以适当的规范和简化。有限元分析模型中最为重要的一步是选择单元类型并划分有限元网格,通常选择壳体类单元描述板料的变形。
3.计算回弹的数学方法
利用隐式算法分析回弹的模型有两种,即:无模法和有模法。采用有模法时,因为仍有接触计算,计算时间比无模法长,而且许多计算结果表明,无模法和有模法得到的回弹量大小几乎完全一致。因此,多数板成形模拟软件(例如Dynaform)在分析制件回弹时采用的是无模法。无模法的计算思路为:在制件冲压成形结束时,去除模具,使所有和模具接触的节点均转变成为自由节点;然后,根据弹塑性有限元法计算得到的最后一步加载结果,按照反向原则,将其结果数据转化为卸载过程节点力的初始值。由于板料零件此时处于无边界约束状态下,为防止出现刚体位移,需要施加位移以及转动约束边界条件。这样,回弹模拟结束后,各节点的位移量即为回弹量。

实验过程及分析
1.拉深成形后的回弹结果分析
图1所示发动机罩的开口四周是全封闭结构,加之制件拉深深度较大(356mm),塑性变形充分,因此可以预见,机罩拉深件切边前的回弹量不会太大。下面通过回弹数值模拟实验加以检验。
(1)回弹实验过程 在Dynaform中进行机罩回弹分析时通常采用dynain方法。dynain方法一般分为两步,首先利用有限元动力显式算法求解制件的成形过程,并将最终计算结果中的制件厚度、应力应变分布等信息写入dynain文件;然后把该文件导入回Dynaform,设置好回弹计算条件,再提交给Dynaform的动力隐式求解器进行回弹计算。具体做法如下:打开Dynaform前处理,导入成形计算得到的dynain模型(见图4)。因为制件成形过程中存在多次自适应网格划分,所以模型中较大变形区域的网格较密。
回弹计算时要求排除被分析对象的所有刚性运动,若不加以约束,则任何一个很小的载荷都将导致分析对象无限制地作刚性运动而不产生回弹应力。无约束刚体运动包括3个平动和3个转动,当采用转动自由度来约束时,在计算中会带来截断误差问题,所以用约束3个节点的平动自由度来约束整个制件的刚性运动,同时也间接地约束了制件的转动。这3个约束节点的选择必须满足一定要求:不能在一条直线上;不要靠近零件的边缘;不要选取变形较大的区域;相互之间要隔开一定的距离。图5所示是在拉深件上选择3个约束节点的位置,3个节点分别座落在机罩顶部座椅凹槽平面和两侧平面的中心处。

(2)回弹模拟结果分析 打开Dynaform的后处理器,选择回弹计算得到的结果文件d3plot。由于在回弹计算时采用的是单步隐式算法,所以在d3plot文件中只有制件回弹前的初始状态和制件回弹后的终了状态。如图6所示,第一帧、第二帧分别代表制件回弹前后的外形(X-Z视图)。
根据制件回弹前后的外形变化,可以发现制件凸缘区有微小回弹变形。为了更加清楚的观察回弹情况,分别按图7方式选取四个截面A-A、B-B、C-C、D-D,以分析机罩拉深件回弹前后的轮廓线变化。
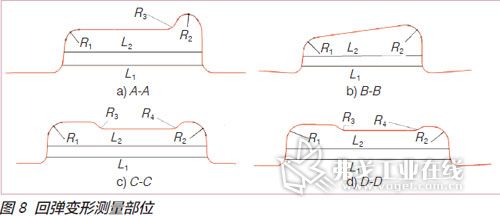
轮廓线上靠近凸缘区的口部容易回弹,导致口部尺寸增大。在机械设计中,轮廓口部尺寸有技术公差要求,由于装配要求,口部尺寸必须控制在一定公差范围内。圆角部位也是回弹趋势较大区域,所以必须测量圆角部位回弹前后的尺寸大小。各截面轮廓回弹变形的测量部位如图8所示,其回弹前后的测量数据汇总在表中。
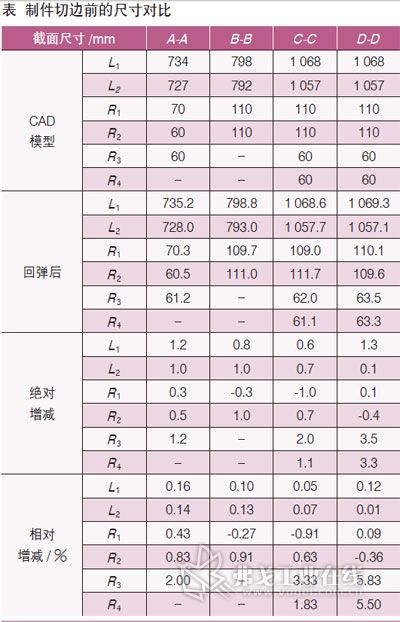
通过对表中的数据分析发现:回弹后绝对增减值非常小,相对增减(%)值也非常小,但是尺寸变化有正有负,说明拉深制件存在微量扭曲现象。
对机罩零件的回弹研究表明:由于机罩零件既不属于类U形弯曲件,又不属于浅拉深为主要变形方式的小曲率件,而是属于空间形状较复杂、拉深深度较大(356mm)的盒形件,加之零件的板料厚度较大(1.5mm),塑性变形充分,拉深件内部的应力应变分布合理,各区的弹复变形存在相互制约现象,所以机罩的回弹变形很小,其回弹量没有超出技术要求范围。
结语
对机罩外板零件的回弹研究表明:尽管机罩外板零件属于空间形状较复杂、尺寸较大的盒形件,但由于其拉深深度较大,板料较厚,因此其塑性变形充分,拉深件内部的应力应变分布合理,各区的弹性变形存在相互制约现象,所以机罩零件拉深后的回弹变形很小,其回弹量没有超出技术要求范围,这与有限元模拟结果是一致的。
利用有限元模拟技术准确地预测了发动机罩外板冲压成形过程中回弹现象,这为研究冲压成形工艺及优化设计提供了有力的手段。

